2 - Arithmétique en Python

Exercice 1 || Solution

Donner un algorithme en Python qui test si un entier n donné est pair ou impair.

Exercice 2 || Solution

Donner un algorithme Python qui prends en entrée un couple de deux entiers (p, q) et qui renvoie True si q est un diviseur de p et False si non.

Exercice 3 || Solution

Donner un algorithme en Python qui prends en entré un entier n et qui renvoie la somme s = 1+2+3+ ... +n.

Exercice 4 || Solution

Donner un algorithme en Python qui prends en entrée le nombre de jours d'une vacance jours_vacance et renvoie la durée en minutes.

Exercice 5 || Solution

Ecrire un algorithme en Python qui prend en entrée un entier n supérieur ou égale à 10 et renvoie le chiffre des dizaines de n.

Exercice 6 || Solution

Donner un algorithme en langage Python qui prends en entrée un entier n et renvoie la liste des diviseurs de n.

Exercice 7 || Solution

Ecrire un algorithme en langage Python qui prends en entrée un entier n et renvoie la somme des diviseurs de n.

Exercice 8 || Solution

Écrire un programme en Python pour trouver le plus grand commun diviseur (PGCD) de deux nombres entiers.

Exercice 9 || Solution

En utilisant l'exercice 6, créer un algorithme en python qui prend en entrée un entier n et renvoie le plus petit diviseur strict p de n. p est -il premier?

Exercice 10 || Solution

Créer un algorithme en Python sous forme de fonction qui permet de tester si un entier donné est produit de deux nombres premiers.
Exemple : si n = 10 , la fonction renvoie  True. Si n = 8 la fonction renvoie False.

Exercice 11 || Solution

Les nombres premiers de Chen sont une classe spéciale de nombres premiers, nommée d'après le mathématicien chinois Chen Jingrun.  Un nombre premier p est appelé un nombre premier de Chen si +2 est soit un autre nombre premier, soit le produit de deux nombres premiers distincts (c'est-à-dire un nombre semi-premier).
Ecrire un algorithme sous forme de fonction qui prends en paramètre un entier n et renvoie la liste des nombres premiers de Chen p<=n.
Exemple: si n = 45, l'algorithme renvoie la liste [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41] (43 est un nombre premier qui n'est pas de Chen)

Exercice 12 || Solution

Écrire un algorithme en langage Python sous forme de fonction qui prend en argument un nombre n >= 100 et qui renvoie la liste des diviseurs de n de la forme d = pq avec p+q est premier Exemple pour n = 100 l'algorithme renvoie la liste [20, 25, 50].

Exercice 13 || Solution

Ecrire un programme en langage Python qui retourne la liste des nombres entiers formés de trois chiffres n = pqr avec q et r sont premiers entre eux.

Exercice 14 || Solution

Ecrire un programme en langage Python qui prend en entrée un entier n et renvoie la liste des chiffres qui composent cet entier n. Exemple pour n = 7352, l'algorithme doit renvoyer la liste : [2, 5, 3, 7].

Exercice 15 || Solution

Ecrire un programme en langage Python qui prend en entrée un entier n et renvoie la liste des chiffrespremiers qui composent cet entier n. Exemple pour n = 34796, l'algorithme doit renvoyer la liste : [7, 3].

Exercice 32 || Solution

Un nombre entier est dit heureux si, lorsqu'on calcule la somme des carrés de ses chiffres dans son écriture en base dix puis la somme des carrés des chiffres du nombre obtenu et ainsi de suite, on obtient à la fin le nombre 1. Un nombre est malheureux lorsque ce n'est pas le cas.

Exercice 33 || Solution

On appelle nombres premiers jumeaux, deux nombres premiers dont la différence est égale à 2. Exemple: les couples de nombres suivants sont des nombres premiers jumeaux (3 , 5) , (5 , 7), (11, 13). par contre (13, 17), (19, 23) sont des couples de nombres premiers qui ne sont pas jumeaux!

Ecrire un algorithme sous forme de fonction qui détermine la liste des couples d'entiers premiers jumeaux inférieur ou égaux à un entier n passé en paramètre

Exercice 34 || Solution

Un nombre premier p est dit nombre premier de Sophie Germain si 2p + 1 est aussi un nombre premier. Exemple: p = 5 est un nombre premier de sophie german car 2p + 1 = 2x5 + 1 = 11 est aussi premier et q = 7 est un nombre premier qui n'est pas de sophie german Ecrire un programme en langage Python sous forme de fonction qui prend en entrée un entier n et renvoie la liste des nombres premiers de sophie german qui sont inférieur ou égaux à n.

Exercice 35 || Solution

Écrire un programme en Python qui prend en entrée un nombre entier, n. Le programme doit identifier et afficher la liste de tous les entiers parfaits qui sont inférieurs ou égaux à n. Un nombre parfait est un entier positif égal à la somme de ses diviseurs propres (excluant lui-même).

Exercice 36 || Solution

Ecrire un programme en python sous forme de fonction qui prend en entrée un nombre n. Ensuite, le programme doit générer et afficher la liste de couples d'entiers (p, q) tels que la somme p + q soit un nombre parfait et inférieure ou égale à n.

Exercice 37 || Solution

Un entier n est qualifié de nombre de Leyland s'il peut être représenté par l'équation n = p^q + q^p. Voici un programme en Python qui prend en entrée un nombre entier et vérifie s'il appartient à la catégorie des nombres de Leyland.

Exercice 38 || Solution

Dans le contexte des nombres parfaits, un nombre parfait est un nombre entier positif qui équivaut à la somme de ses diviseurs propres positifs, excluant le nombre lui-même. Les diviseurs propres d'un nombre se réfèrent à ses diviseurs autres que le nombre lui-même.

Prenons l'exemple du nombre 28 : il est considéré comme parfait car la somme de ses diviseurs propres donne 1 + 2 + 4 + 7 + 14 = 28. Les premiers nombres parfaits sont 6, 28, 496 et 8128. Ces nombres présentent des propriétés mathématiques intrigantes et ont été étudiés depuis l'Antiquité. En résumé, un nombre parfait est un entier dont la somme de ses diviseurs propres, à l'exception de lui-même, est égale à lui-même.

À des fins pratiques, définir un algorithme en python qui, lorsqu'il prend en entrée un nombre entier, renvoie True s'il s'agit d'un nombre parfait et False sinon.

Exercice 39 || Solution

Un nombre pronic, également désigné comme nombre rectangulaire, est un nombre entier qui se manifeste en tant que produit de deux nombres consécutifs. Sur le plan mathématique, un nombre pronic peut être formulé comme n*(n + 1), où "n" est un nombre entier. Autrement dit, un nombre pronic suit la forme n² + n. Par exemple, examinons le nombre 12. Il peut être décomposé en tant que produit de 3 * 4, où 3 et 4 sont des nombres consécutifs. Écrire un programme en Python qui sollicite un nombre entier en entrée et détermine s'il s'agit d'un nombre de Pronic (nombre rectangulaire).

Exercice 40 || Solution

Ecrire un programme en langage Python qui demande à l'utilisateur de saisir un entier n et de lui renvoyer le message indiquant que le nombre tapé est premier ou non selon l'entier saisi au clavier.

Exercice 41 || Solution

Écrire un algorithme python sous forme de fonction qui prend en argument deux entiers m et n qui retourne la liste de tous les diviseurs communs à m et n.

Exercice 42 || Solution

Écrire un algorithme Python sous forme de fonction qui prend en argument un entier n et renvoie le plus grand entier premier inférieur ou égal à n. Exemple pour n = 15, la fonction renvoie le plus grand nombre premier inférieur ou égal à 15, soit 13.

Exercice 43 || Solution

Écrire un algorithme Python sous forme de fonction qui prend un entier n comme argument et renvoie le plus petit entier premier supérieur ou égal à n. Exemple pour n = 8, la fonction renvoie le plus petit nombre premier supérieur ou égal à 8 qui est 11.

Exercice 44 || Solution

Écrire un algorithme en Python sous forme de fonction qui prend en argument un entier positif n et retourne la liste de tous les tuples (u, v) d’entiers tels que : u² + v² ≤ n.

Exercice 45 || Solution

Écrire un programme en Python qui déterminer la liste des diviseurs impairs du nombre 3570 qui sont multiples de 3 et contenus dans l'intervalle [500, 2500].

Exercice 46 || Solution

Écrire un programme en Python qui trouve le plus petit diviseur strictement supérieur à 1 d'un entier positif donné n.

Exercice 47 || Solution

Écrire un programme en Python qui recherche le plus grand diviseur stricte d'un entier positif donné n. Exemple pour n = 18, le plus grand diviseur de n est 9.

Exercice 48 || Solution

Écrire une fonction en python qui prends en arguments deux nombres entiers a et b et qui renvoie un tuple formé de :

1. Le quotient q de la division euclidienne de a par b (sans utiliser l'opérateur // )
2. Le reste r de la division euclidienne de a par b (sans utiliser l'opérateur % )

Exercice 49 || Solution

Écrire une fonction en python qui prends en arguments deux nombres entiers a et b et qui renvoie le PGCD de a et b sans utiliser aucune fonction prédéfinie en python.

Exercice 50 || Solution

Écrire une fonction en python qui prends en arguments deux nombres entiers a et b et qui renvoie le PPCM de a et b sans utiliser aucune fonction prédéfinie en python

Exercice 52 || Solution

Écrire un algorithme sous forme de fonction en Python qui prends en argument un entier n et qui renvoie True si l'entier n est premier et False si non.

Exercice 53 || Solution

Écrire un algorithme en Python sous forme de fonction qui prends deux nombres m et n en paramètres (m<n) et qui renvoie une liste formée de tous les nombres premiers compris entre m et n. Exemple pour m=10 et n=20 la fonction doit renvoyer [11 , 13 , 17 , 19]

Exercice 54 || Solution

Écrire un algorithme sous forme de fonction en Python qui prends en argument deux nombres entiers a et b et lui renvoie True si les nombres sont premiers entre eux et False si non.

Exercice 55 || Solution

Écrire un algorithme en Python qui demande à l'utilisateur de tapez deux nombres entiers a et b premiers entre eux et lui renvoie un tuple (u,v) vérifiant: ua + vb = 1 (identité de Bezout)

Exercice 56 || Solution

Déterminer la liste des diviseurs impairs du nombre 3570 qui sont multiples de 3 et contenus dans l'intervalle [500, 2500]

Exercice 57 || Solution

En utilisant la bibliothèque Python Tkinter , écrire un programme Python permettant d'afficher à l'utilisateur une boite de dialogue lui demandant de saisir un nombre entier et de lui renvoyer son double: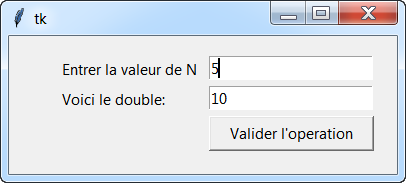

Exercice 58 || Solution

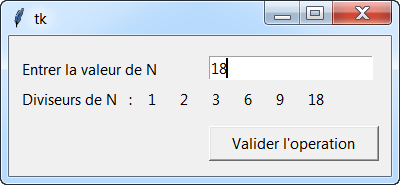
1. Écrire un programme en Python qui permet de lister les diviseurs d’un entier N donné.
2. En utilisant la première question, créer un programme en Python qui propose à l’utilisateur une fenêtre Tkinter lui demandant de saisir un entier N et lui renvoie tous les diviseurs de N.

Exercice 59 || Solution

En utilisant les exercices précédents 49 et 50, créer une interface graphique Tkinter, permettant de calculer le pgcd et le ppcm graphiquement comme le montre la figure ci-dessous :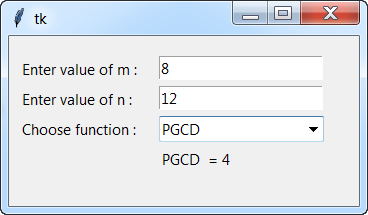

Exercice 60 || Solution

Ecrire un algorithme en python qui demande à l'utilisateur de saisir un entier n et qui renvoie la liste des entiers positifs  p tels que   n < p² < 3*n².

Exercice 61 || Solution

Écrire un algorithme en python qui renvoie la liste des entiers positifs composés de de deux chiffres de la forme pq tel que le produit des chiffres p*q est un multiple de leur somme p + q (avec p et q sont non nuls).

Exercice 62 || Solution

Ecrire un algorithme python qui demande à l'utilisateur de taper un entier n et de lui renvoyer la liste des entiers p <= n dont le dernier chiffre 3 ou 7. Exemple: si l'utilisateur saisi l'entier n = 20, l'algorithme lui renvoie la liste: L = [3 , 7 , 13 , 17 ]

Exercice 63 || Solution

Ecrire un programme en python qui affiche tous les nombres entiers positif composés de deux chiffres n = pq telle que la somme des chiffres p+q est un multiple de 5.

Exercice 64 || Solution

Ecrire un programme en python permettant de trouver la liste des diviseurs premiers d'un nombre entier.

Exercice 65 || Solution

Ecrire un programme en python qui demande à l'utilisateur de saisir un nombre entier n <= 100 et de lui afficher la liste des nombres premiers <= n dont la somme des chiffres est pair. Exemple si l'utilisateur saisi n = 40, le programme renvoie la liste: [11, 13, 17, 19, 31, 37].

Exercice 66 || Solution

Ecrire un programme en python sous forme de fonction qui prends en paramètres deux entiers m et n et qui renvoie la liste des diviseurs communs à m et n. Exemple si n = 18 et m = 27 , la fonction renvoie la liste:[1, 3, 9]

Exercice 67 || Solution

Ecrire un algorithme en python qui renvoie la liste des diviseurs premiers communs à deux entiers.

Exercice 68 || Solution

Ecrire un algorithme en python qui renvoie pour un entier donné n,  la liste des tuples (p , q) formés des entiers premiers  p et q vérifiant p + q == n .

Exercice 69 || Solution

Algorithme en python qui détermine la somme des diviseurs propres d'un entier n. Exemple pour n = 10, les diviseurs propres sont  1 ,  2  et   5  et par suite l'algorithme renvoie la somme 1 + 2 + 5 = 8.

Exercice 70 || Solution

Ecrire un programme en python sous forme de fonction qui teste si deux nombres m et n sont amis ou non. Rappel On dit que deux nombres entiers naturels non nuls m et n sont amis ou amicaux si chacun de ces deux nombres est égal exactement à la somme des diviseurs stricts(diviseurs autres que lui-même) de l'autre. Exemple n = 220 , la somme des diviseurs de l'entier n (en éliminant 220) : 1+2+4+5+10+11+20+22+44+55+110=284 m = 284 , la somme des diviseurs de l'entier m (en éliminant 284) : 1+2+4+71+142=220 et par suite m et n sont amis.

Exercice 71 || Solution

La suite de Fibonacci est une suite récurrente  dans laquelle chaque terme est obtenu en additionnant les deux termes qui le précèdent, elle est ainsi définie par :

---

F₀ = 0 F₁ = 1 F_n+2 = F_n+1 + F_n

---

Créer un algorithme en python sous forme de  fonction  qui renvoie le (n+1)^ème terme de la suite de Fibonacci pour un entier n donné, puis donner un algorithme qui affiche les 10 premiers termes de la suite de Fibonacci.

Exercice 72 || Solution

Ecrire un algorithme en python sous forme de fonction qui prends en paramètres un entier n et qui renvoie la liste des couples (p , q) formés des entiers p et q  vérifiant:

1. p et q sont deux diviseurs de n
2. p + q est premier.

Exemple  si n = 10 , l'algorithme renvoie la liste:  [(1, 1), (1, 2), (2, 1), (2, 5), (5, 2)]

Exercice 73 || Solution

Ecrire un algorithme en python qui détermine pour un entier n donné les couples (p , q) vérifiant:

1. p premier avec q
2. p < q <= n

Exercice 74 || Solution

Ecrire un algorithme en python qui détermine pour un entier n donné les couples (p , q) vérifiant:

1. p et q sont positifs non nuls et  p < q <= n
2. p et q ne sont pas premiers entre eux et pgcd(p , q)<= 10

Exercice 75 || Solution

Ecrire un algorithme en python qui détermine pour un entier n donné les couples (p , q)  avec p <= n et q <= n  dont le plus grand diviseurs commun pgcd(p,q) est premier.

Exercice 76 || Solution

Ecrire un algorithme en python sous forme de fonction qui prends en paramètres un entier naturel n et qui renvoie la liste des nombres premiers dont le chiffre des dizaines est premier. Exemple pour n = 100 , l'algorithme renvoie la liste: [23, 29, 31, 37, 53, 59, 71, 73, 79]

Exercice 77 || Solution

Ecrire un algorithme python qui teste pour un entier n >= 10 si le chiffre des dizaines de n est premier avec celui des unités de n.

Exercice 78 || Solution

Ecrire un programme python qui renvoie pour un entier n >= 10 donné la liste des entiers premiers <= n dont le chiffre des dizaines n'est pas premier !

Exercice 79 || Solution

On dit qu'un nombre entier est distinct, s'il est composé de chiffres tous distincts deux à deux. Exemple: n = 123456  est distinct. Tandis que m = 224544 ne l'est pas puisque les chiffres qui le composent ne sont pas tous distincts. Ecrire un algorithme python sous forme de fonction qui prends en paramètre un entier n et renvoie True si l'entier n est distinct et False si non.

Exercice 80 || Solution

Ecrire un programme en Python qui renvoie la liste de tous les entiers formés de deux chiffres pq vérifiant: la somme p+q est un diviseur du produit pq.

Exercice 81 || Solution

Ecrire un algorithme en Python qui renvoie la liste de tous les entiers formés de deux chiffres pq vérifiant: la somme p+q est un diviseur premier du produit pq.

Exercice 82 || Solution

Ecrire un algorithme en python qui renvoie pour un entier donné la somme de ses diviseurs premiers. Exemple pour n = 10, l'algorithme renvoie la somme 2 + 5  = 17    

Younes Derfoufi CRMEF OUJDA